Estimating Autocorrelation of Colored Noise
Julia Pilowsky
2020-10-08
Source:vignettes/noise.Rmd
noise.RmdWhat is colored noise?
Expressed in plain words, colored noise is a stochastic process wherein values tend to be correlated with other values nearby in space or time. Colored noise in spatial data sets is said to be spatially autocorrelated, while colored noise in time series is said to be temporally autocorrelated. In this package we only deal with the latter.
Expressed in math, colored noise can be modeled with the following equation, where \(\omega\) is a random standard normal variable, and \(\epsilon\) is a temporally autocorrelated variable:
\(\epsilon_{t + 1} = k\epsilon_t + \omega_t\sqrt{1 - k^2}\)
Mathematically, we can also think of unautocorrelated stochasticity as random sine waves evenly distributed across all wavelengths, while autocorrelated stochasticity is biased either toward sine waves of long wavelengths (red) or short wavelengths (blue).
Expressed graphically, colored noise looks like this:
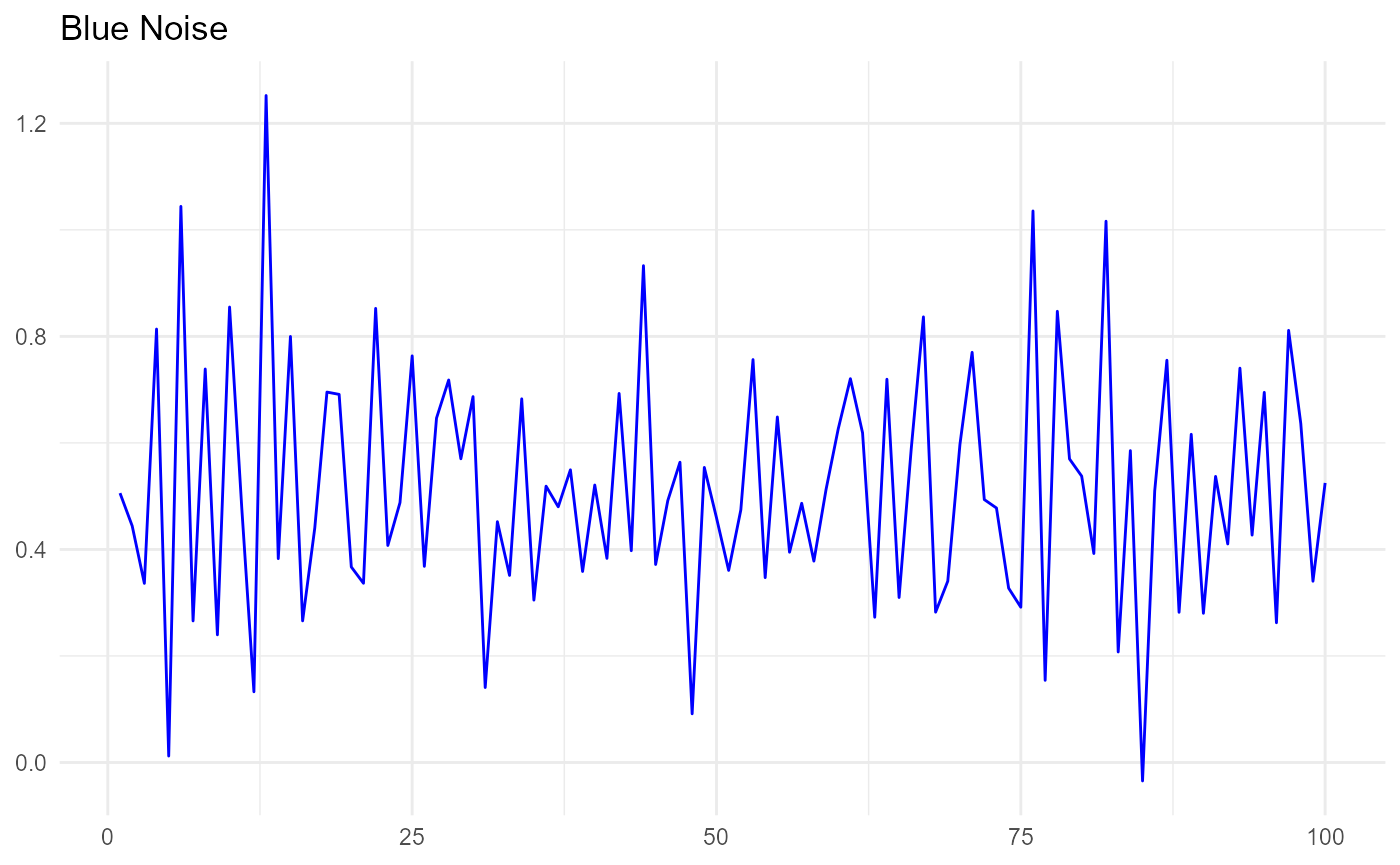
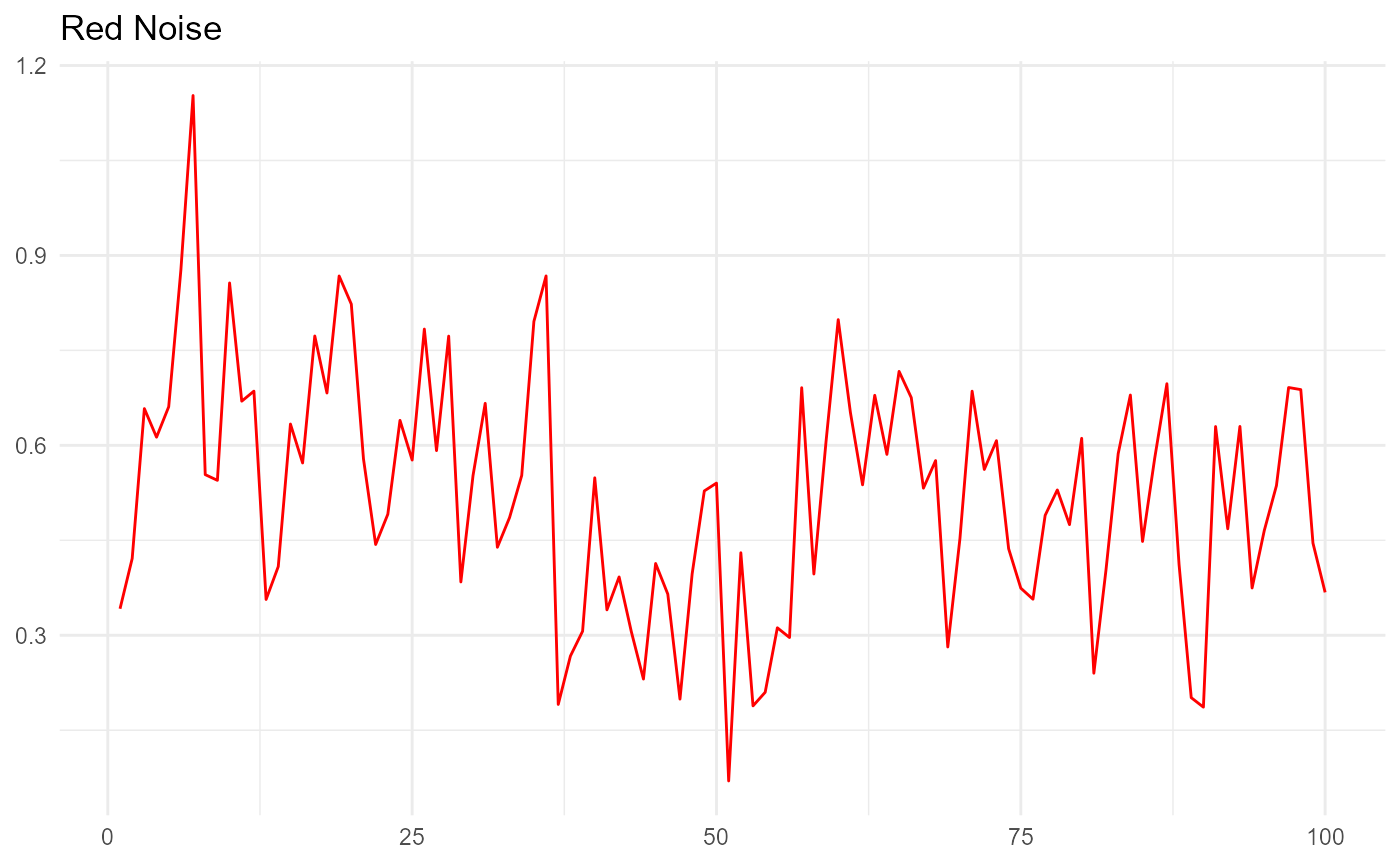
In the blue noise plot above, each random number is negatively correlated to the one preceding it. In the red noise plot, each random number is positively correlated to the one preceding it.
Example: Bias and precision of autocorrelation estimates
To show you how you can use this package to simulate and analyze colored noise, I will present a problem for us to solve. Let’s say we want to find out whether our estimates of temporal autocorrelation are biased when the standard deviation of the colored noise is high. First, let’s use the raw_noise function to generate some colored noise with high variance.
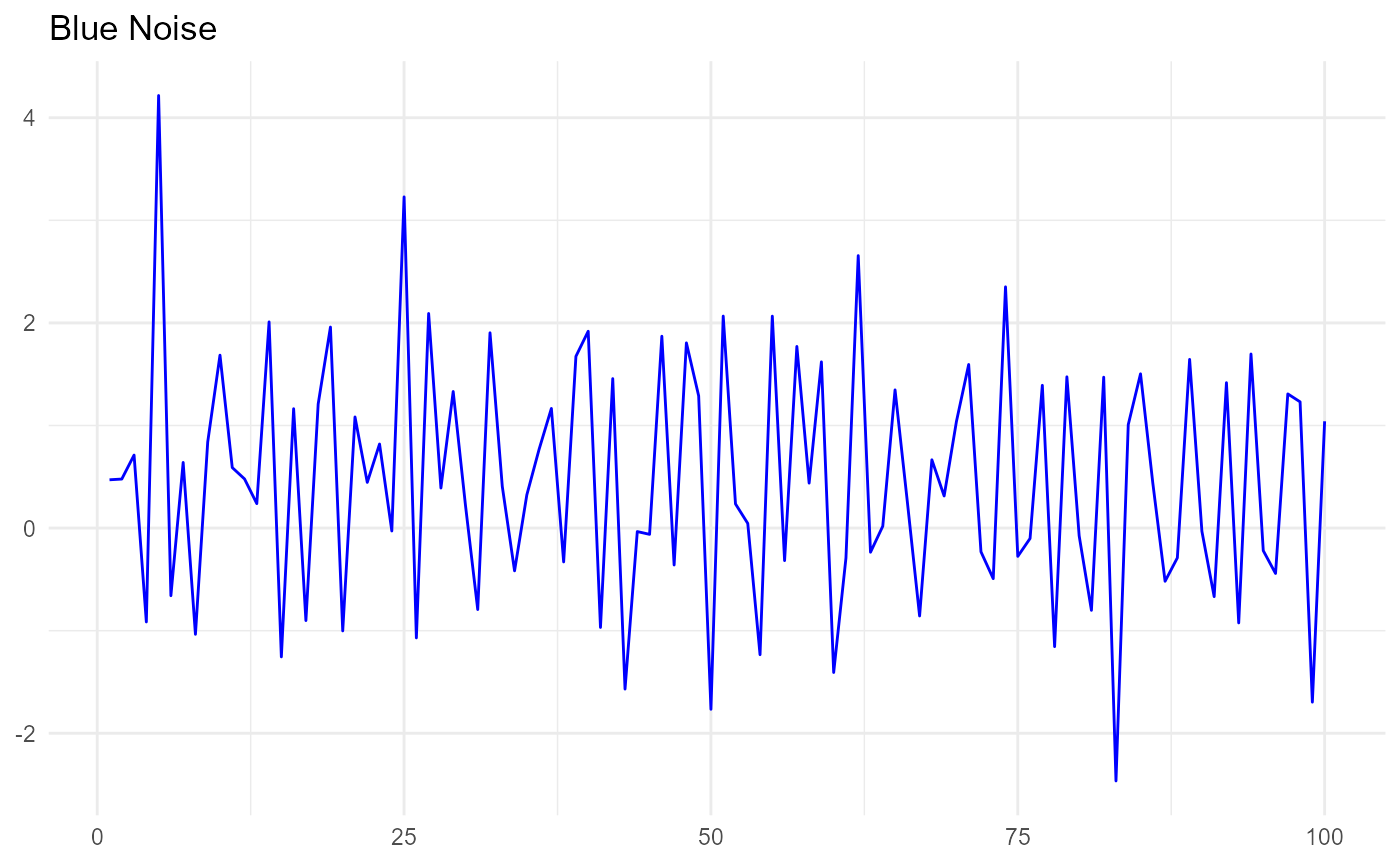
red <- colored_noise(timesteps = 100, mean = 0.3, sd = 1.2, phi = 0.5) red[1:10] #> [1] -3.3556902 -2.6656854 -2.1272799 0.9793865 1.8727956 0.8286511 #> [7] -0.7089789 2.0338977 0.4539040 1.9070181 blue <- colored_noise(timesteps = 100, mean = 0.3, sd = 1.2, phi = -0.5) blue[1:10] #> [1] 0.4708098 0.4779904 0.7116479 -0.9150298 4.2168258 -0.6592254 #> [7] 0.6400465 -1.0357057 0.8387268 1.6858232 ggplot(data = NULL, aes(x = c(1:100), y = blue)) + geom_line(color="blue") + theme_minimal() + theme(axis.title = element_blank()) + ggtitle("Blue Noise")
ggplot(data = NULL, aes(x = c(1:100), y = red)) + geom_line(color="red") + theme_minimal() + theme(axis.title = element_blank()) + ggtitle("Red Noise")
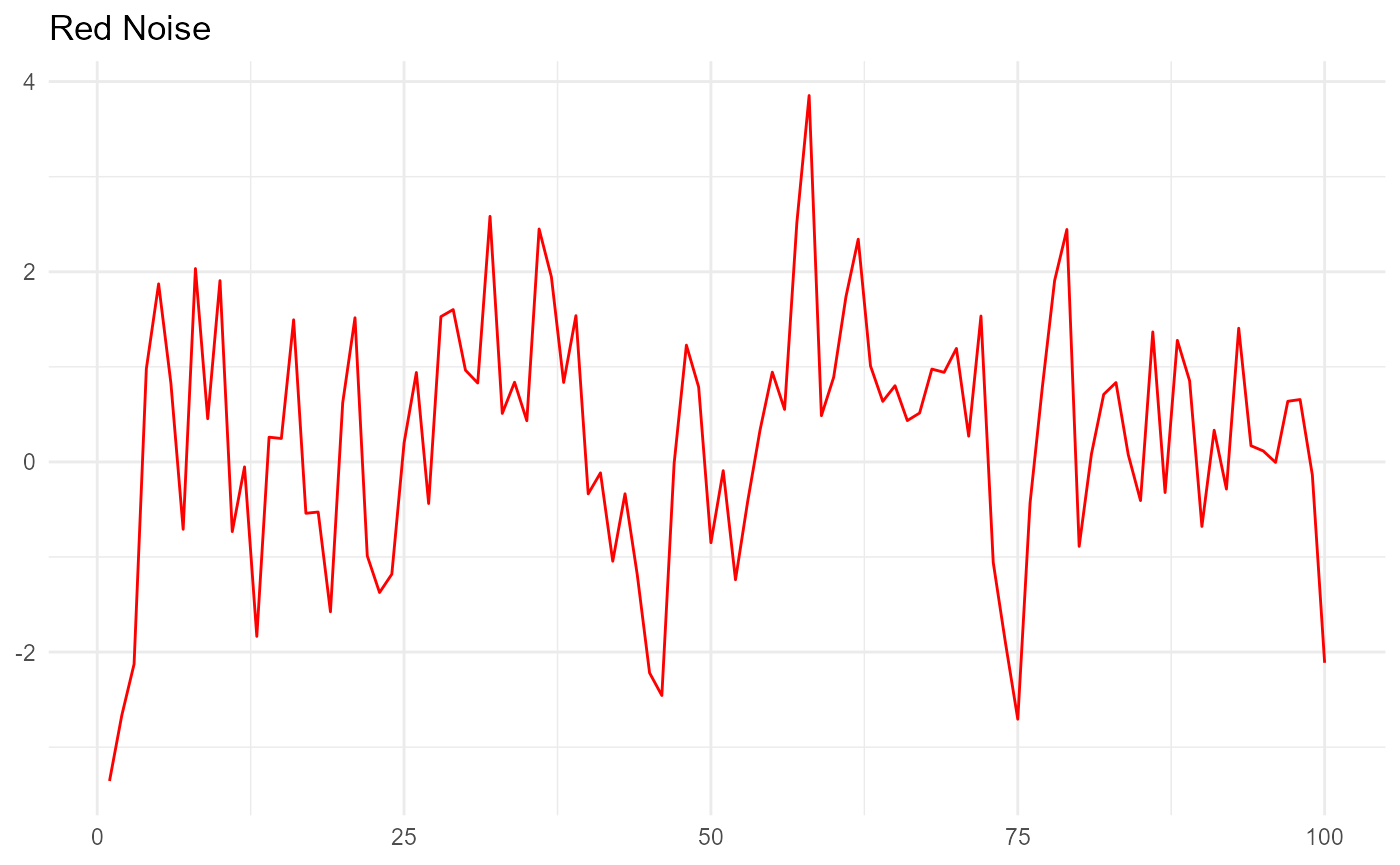
The red noise and blue noise look the way they should. Now let’s estimate the mean, SD, and autocorrelation of these two sets of random numbers to see how well they match the parameters we used to generate them.
invoke_map(list(mean, sd, autocorrelation), rep(list(list(red)), 3)) #> [[1]] #> [1] 0.2771024 #> #> [[2]] #> [1] 1.306311 #> #> [[3]] #> [1] 0.4317427 invoke_map(list(mean, sd, autocorrelation), rep(list(list(blue)), 3)) #> [[1]] #> [1] 0.4710391 #> #> [[2]] #> [1] 1.191427 #> #> [[3]] #> [1] -0.4948799
The estimates for these seem to be quite accurate. But let’s try generating a whole lot of colored noise across a range of variance and color and estimating the autocorrelation of each replicate.
raw_sims <- cross_df(list(timesteps = 20, phi = c(-0.5, 0, 0.5), mean = 0.3, sd = c(0.5, 0.7, 0.9, 1.1, 1.3, 1.5))) %>% rerun(.n = 30, pmap(., colored_noise)) labels <- raw_sims %>% map(1) %>% rbindlist() noise <- raw_sims %>% map(2) %>% flatten() estimates <- data.table(mu = map_dbl(noise, mean), sigma = map_dbl(noise, sd), autocorrelation = map_dbl(noise, autocorrelation)) sd_range <- cbind(labels, estimates) head(sd_range) #> timesteps phi mean sd mu sigma autocorrelation #> 1: 20 -0.5 0.3 0.5 0.3620196 0.5337716 -0.50719389 #> 2: 20 0.0 0.3 0.5 0.5682215 0.5293456 0.01135706 #> 3: 20 0.5 0.3 0.5 0.5752618 0.3305384 0.57798690 #> 4: 20 -0.5 0.3 0.7 0.1253258 0.6800782 -0.44375225 #> 5: 20 0.0 0.3 0.7 0.1635260 0.6481182 -0.31746752 #> 6: 20 0.5 0.3 0.7 0.2015518 0.5212291 0.35049626
We can visualize these results by finding the mean and confidence intervals of the autocorrelation estimates for each combination of variance and noise color, and plotting them out.
summ <- sd_range[, .(lower.ci = ((function(bar) { quantile(bar, probs = c(0.05, 0.95))[[1]] })(autocorrelation)), upper.ci = ((function(bar) { quantile(bar, probs = c(0.05, 0.95))[[2]] })(autocorrelation)), mean = mean(autocorrelation)), keyby = .(phi, sd)] ggplot(summ, aes(x = sd, y = mean)) + geom_pointrange(aes(ymin = lower.ci, ymax = upper.ci, color = factor(phi)), size = 0.8) + geom_hline(yintercept = 0, linetype = 2, color = "#C0C0C0") + geom_hline(yintercept = -0.5, linetype = 2, color = "#0033FF") + geom_hline(yintercept = 0.5, linetype = 2, color = "#CC0000") + theme(text=element_text(size=20)) + xlab("Standard Deviation") + ylab("Estimated Autocorrelation") + scale_colour_manual(values = c("#0033FF", "#C0C0C0", "#CC0000")) + labs(color="Noise color") + theme_light()
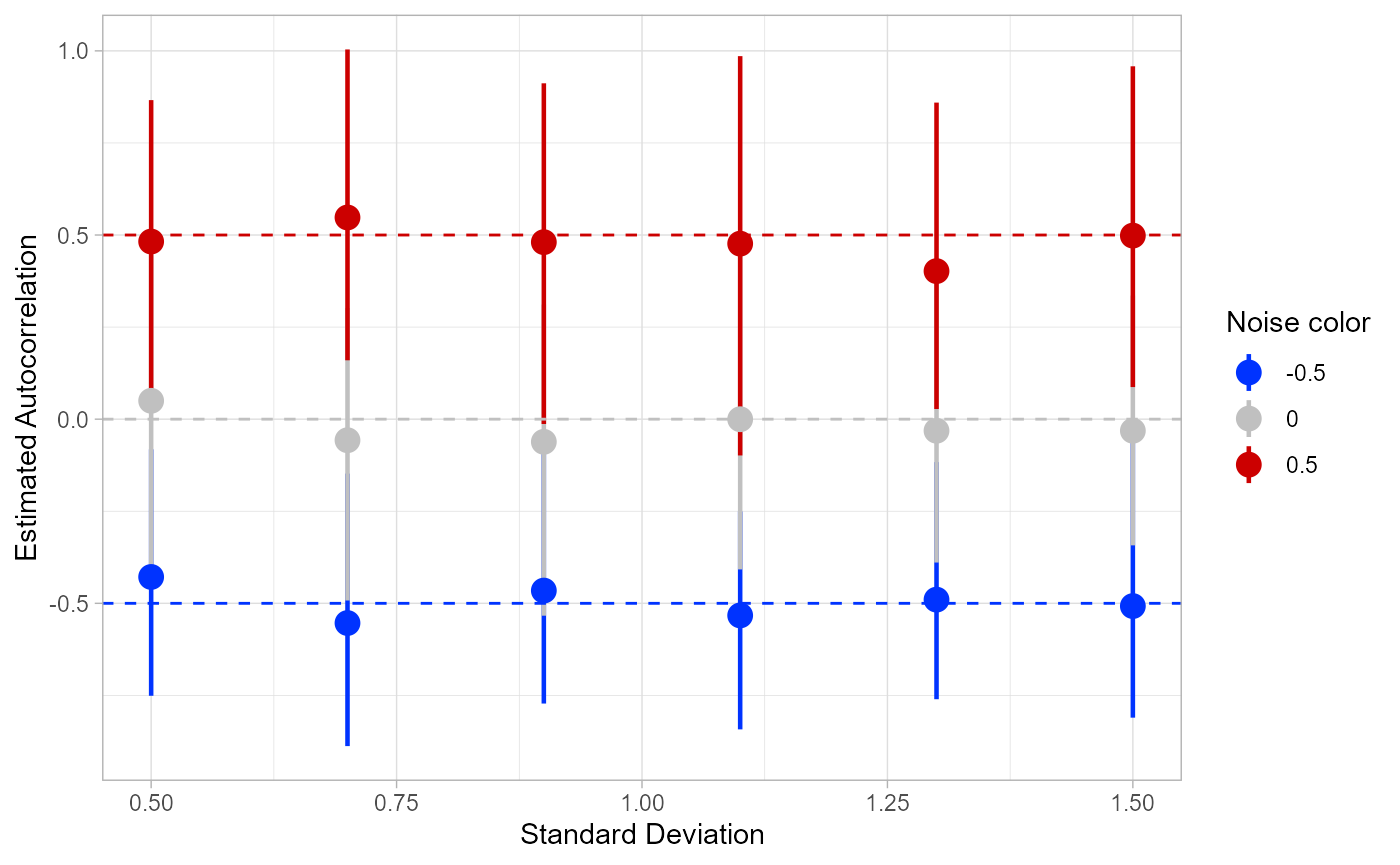
As we can see, the variance of the colored noise does not seem to affect the estimates of autocorrelation in any case. However, another interesting pattern emerges: the estimates of autocorrelation for red noise (phi = 0.5) are consistently biased too low. This may be because the number of timesteps we simulated (20) is too short to get a full measurement of the long wavelengths of red noise.
Let’s explore this possibility further.
Example: Estimating autocorrelation in colored noise populations
We now suspect, based on estimates of colored noise, that long time series are required in order to detect positive temporal autocorrelation without bias. However, the problem becomes even more complex when we use colored noise to simulate populations. Now, the environmental stochasticity we’re modeling as colored noise is compounded by demographic stochasticity, the random drift resulting from the discrete probability distribution of births and deaths, especially in small populations.
To give an example of what I mean, let’s model a small population with positively autocorrelated environmental stochasticity. This population is closed (no migration), assumes constant fertility and mortality for all individuals, and can be thought of as asexually reproducing or female-only.
set.seed(3935) series1 <- unstructured_pop(start=20, timesteps=20, survPhi=0.4, fecundPhi=0.4, survMean=0.5, survSd=0.2, fecundMean=1, fecundSd=0.7) ggplot(series1, aes(x=timestep, y=population)) + geom_line()
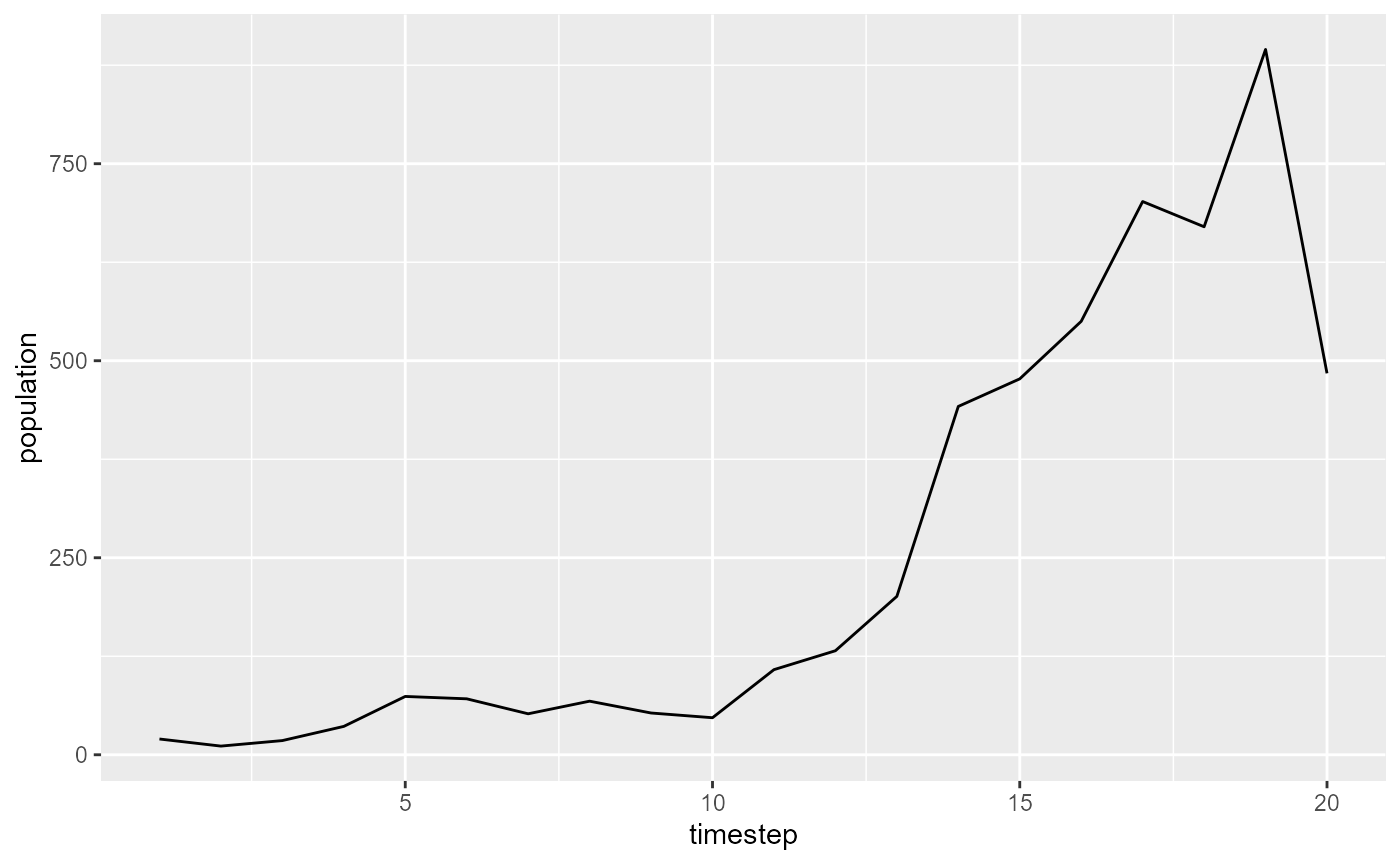
Now let’s try addressing the question of whether short time series bias our estimates of autocorrelation in red noise populations. We can do this by simulating populations along a range of time series lengths and noise color. Let’s try a full range from blue noise to red noise in the survival vital rate, and a range of time series lengths from five years to a hundred years.
sims <- autocorr_sim(timesteps = seq(5, 60, 5), start = 200, survPhi = c(-0.5, -0.25, -0.2, -0.1, 0, 0.1, 0.2, 0.25, 0.5), fecundPhi = 0, survMean = 0.4, survSd = 0.05, fecundMean = 1.8, fecundSd = 0.2, replicates = 100) ggplot(sims[[6]], aes(x=timestep, y=population)) + geom_line()
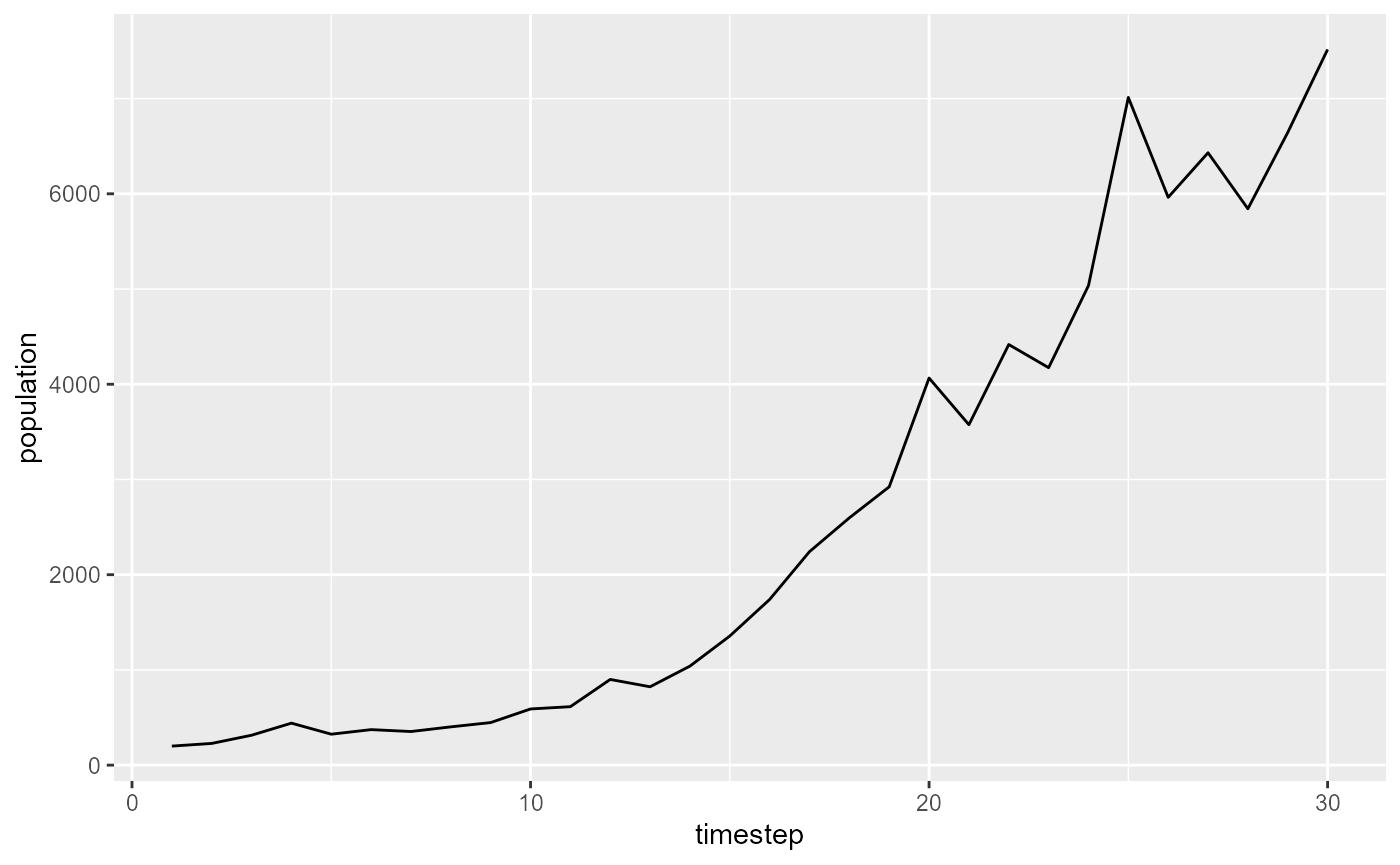
Here we see one example of a population simulated by the function.
Now let’s estimate the autocorrelation in each of these simulated populations. There is a utility function autocorrelation in this package that measures temporal autocorrelation at a time lag of 1.
estimates <- sims %>% map(~.[, .(acf.surv = autocorrelation(est_surv, biasCorrection = F)), keyby = .(survPhi, timesteps)]) %>% rbindlist()
I find that this format of ggplot displays the estimates by noise color very nicely.
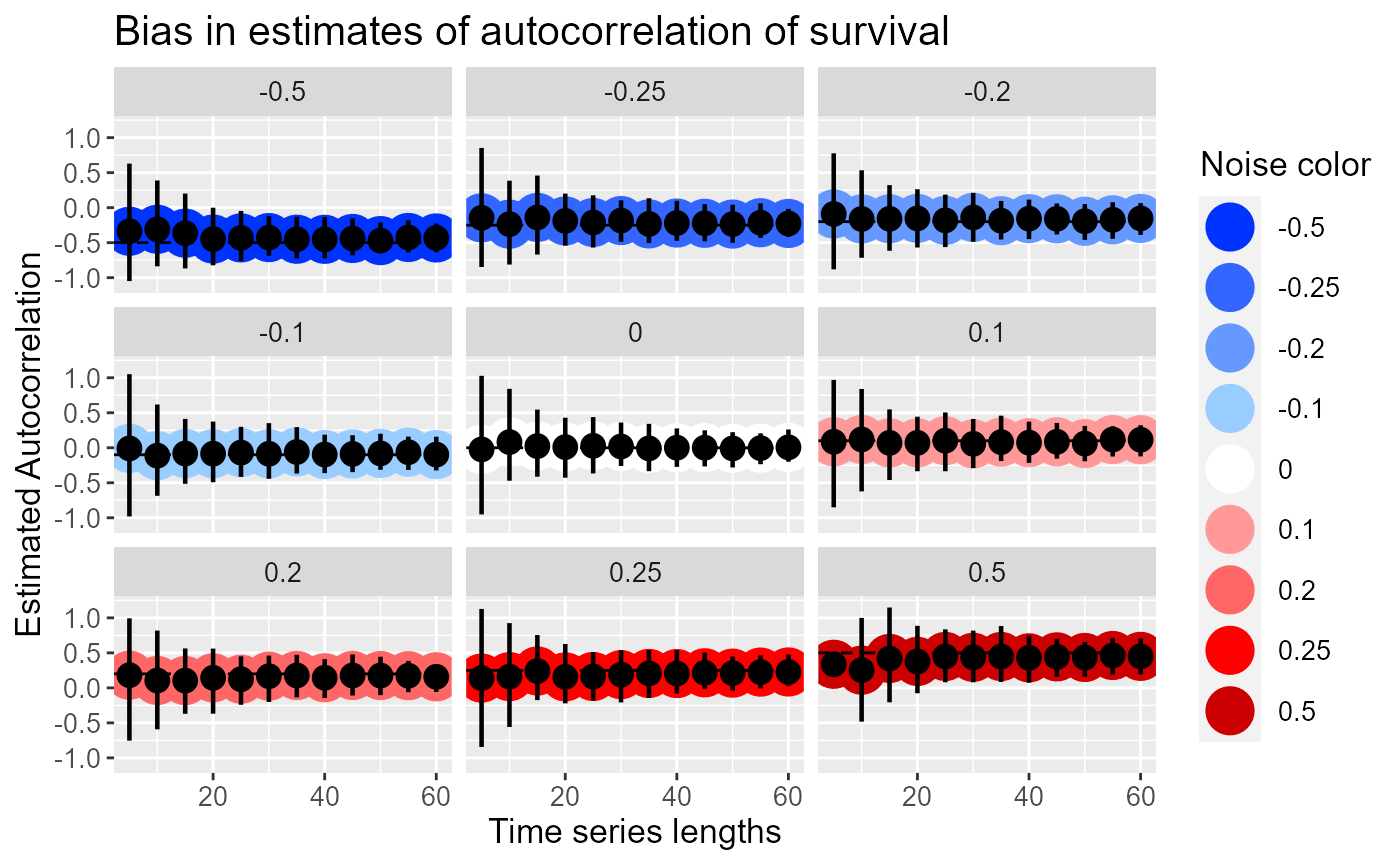
summ2 <- estimates[, .(lower.ci = ((function(bar) { quantile(bar, probs = c(0.05, 0.95))[[1]] })(acf.surv)), upper.ci = ((function(bar) { quantile(bar, probs = c(0.05, 0.95))[[2]] })(acf.surv)), mean = mean(acf.surv)), keyby = .(survPhi, timesteps)] # Noise color values for the graph in hexadecimal noise = c("#0033FF", "#3366FF", "#6699FF", "#99CCFF", "#FFFFFF", "#FF9999", "#FF6666","#FF0000", "#CC0000") ggplot(summ2, aes(x=timesteps, y=mean)) + geom_point(size=8, aes(color=factor(survPhi))) + # This creates confidence intervals around the autocorrelations geom_pointrange(aes(ymin=lower.ci, ymax=upper.ci), size=0.8) + # Adds a line for the true autocorrelation value geom_hline(aes(yintercept=survPhi), linetype=2) + # This facets the plots by true autocorrelation value facet_wrap( ~ survPhi) + # This increases the font size and labels everything nicely theme(text=element_text(size=13)) + xlab("Time series lengths") + ylab("Estimated Autocorrelation") + scale_colour_manual(values=noise) + labs(color="Noise color") + ggtitle("Bias in estimates of autocorrelation of survival") + scale_y_continuous(limits=c(-1.1, 1.2))
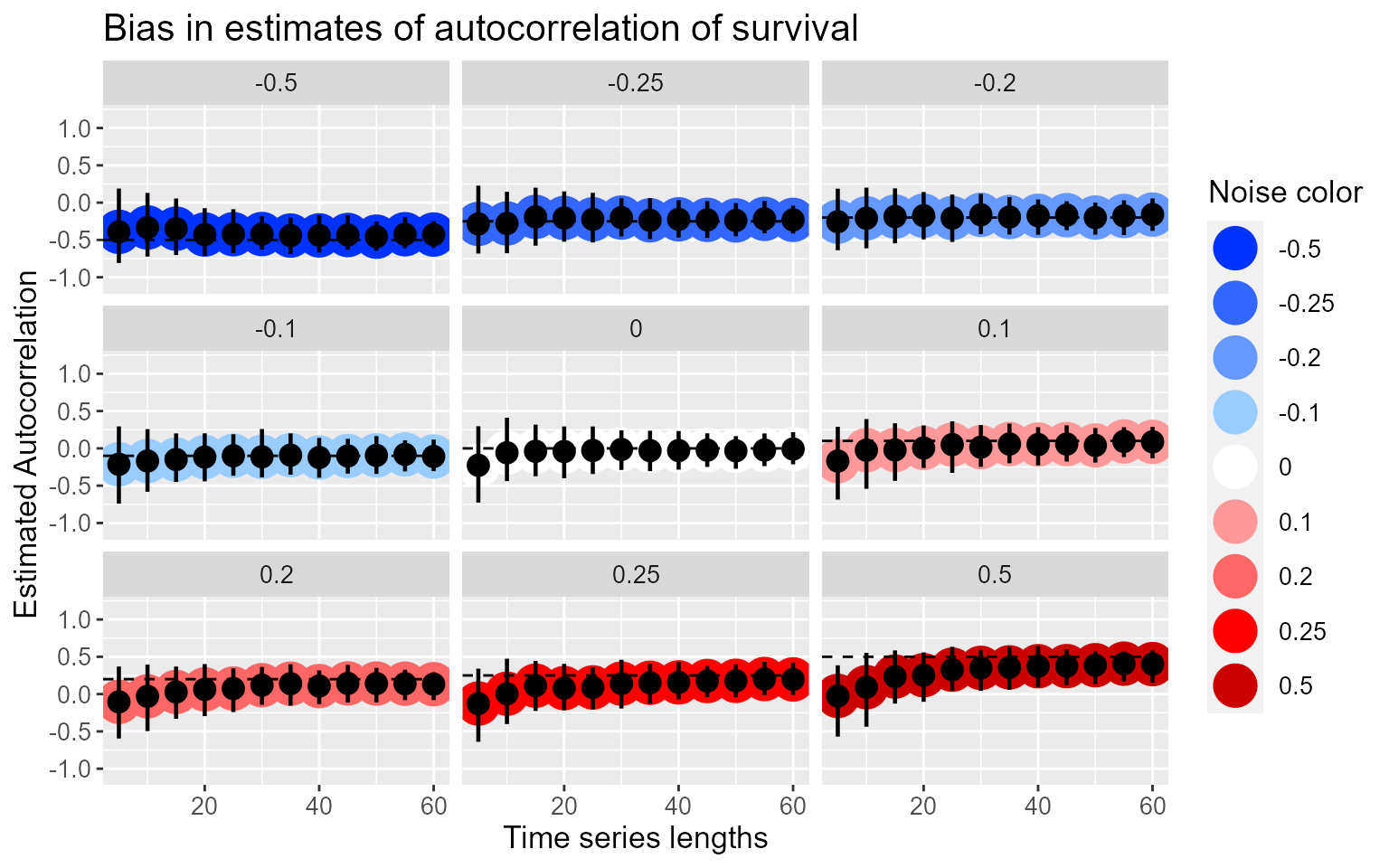 We can see here that autocorrelation estimates are biased negative at short time lengths, especially for populations with positive temporal autocorrelation - when the time series is only 5 timesteps, all of the red noise populations read as white noise populations. When autocorrelation is strongly negative, as in the population at -0.5, short time lengths are slightly positively biased. This matches the findings of M. Kendall in his volume Time-Series, where he showed that there is a bias in autocorrelation estimates such that
We can see here that autocorrelation estimates are biased negative at short time lengths, especially for populations with positive temporal autocorrelation - when the time series is only 5 timesteps, all of the red noise populations read as white noise populations. When autocorrelation is strongly negative, as in the population at -0.5, short time lengths are slightly positively biased. This matches the findings of M. Kendall in his volume Time-Series, where he showed that there is a bias in autocorrelation estimates such that
\[ \hat{\phi} = \phi - \frac{1 + 3\phi}{T - 1} \] where is the autocorrelation and T is the length of the time series.
Correcting the bias
Here is what the autocorrelation estimates look like when I turn on the bias correction in the autocorrelation function.
summ3 <- sims %>% map(~.[, .(acf.surv = autocorrelation(est_surv, biasCorrection = TRUE)), keyby = .(survPhi, timesteps)]) %>% rbindlist() %>% .[, .(lower.ci = ((function(bar) { quantile(bar, probs = c(0.05, 0.95), na.rm=T)[[1]] })(acf.surv)), upper.ci = ((function(bar) { quantile(bar, probs = c(0.05, 0.95), na.rm=T)[[2]] })(acf.surv)), mean = mean(acf.surv)), keyby = .(survPhi, timesteps)] ggplot(summ3, aes(x=timesteps, y=mean)) + geom_point(size=8, aes(color=factor(survPhi))) + geom_pointrange(aes(ymin=lower.ci, ymax=upper.ci), size=0.8) + geom_hline(aes(yintercept=survPhi), linetype=2) + facet_wrap( ~ survPhi) + theme(text=element_text(size=13)) + xlab("Time series lengths") + ylab("Estimated Autocorrelation") + scale_colour_manual(values=noise) + labs(color="Noise color") + ggtitle("Bias in estimates of autocorrelation of survival") + scale_y_continuous(limits=c(-1.1, 1.2)) #> Warning: Removed 1 rows containing missing values (geom_segment).
 The estimates are no longer biased for short time series, though they do become less precise with the bias correction.
The estimates are no longer biased for short time series, though they do become less precise with the bias correction.